|
<< Cliquer pour afficher la table des matières >> Précision sur la distance de recouvrement |
  
|
|
<< Cliquer pour afficher la table des matières >> Précision sur la distance de recouvrement |
  
|
Lors de la création du Terrain, on se trouve confronté d'une part à un volume de données souvent très conséquent et d'autre part à la quantité de mémoire disponible de l'ordinateur (en d'autres termes sa capacité à traiter le volume de données). L'algorithme de création du Terrain de MithraSIG répartit les données en dalles de sorte que chaque dalle contienne un nombre de points acceptable que la mémoire disponible sera en mesure de traiter. Le modèle numérique de terrain sera donc réalisé non pas en un seul TIN mais en plusieurs.
Le tableau suivant indique le nombre de points par dalle qu'il est possible de traiter selon la mémoire disponible :
RAM disponible |
Nombre de points |
500 Mo |
1 000 000 |
1 Go |
2 000 000 |
1.5 Go |
3 000 000 |
2 Go |
4 000 000 |
La mémoire disponible correspond à la part de la mémoire utilisable au moment où on lance la commande et non à la mémoire physique installée. Pour connaître la mémoire disponible, activer l'onglet Performances du Gestionnaire des tâches de Windows et noter la valeur indiquée pour la mémoire physique disponible.
Nous allons étudier un peu plus en détail comment le terrain est créé, en expliquant comment l'algorithme traite les données.
Si on se contentait de créer des dalles adjacentes, on obtiendrait des TIN non jointifs et les triangles du TIN (en rouge sur Exemple de jeu de données ci-après) ne couvriraient en effet pas la totalité de la dalle puisque les triangles en chevauchement (en gris sur Exemple de jeu de données ci-après) ne seraient pas créés (TIN ne couvrant pas toute la dalle).
Ce problème est résolu en utilisant une zone de recouvrement entre les dalles de manière à ce que chaque TIN puisse contenir également les triangles à cheval sur la limite de la dalle. Ainsi les triangles chevauchant les limites de dalles se retrouveront dans les TIN associés à ces dalles. Il y aura donc recoupement des TIN, mais comme ce sont les mêmes triangles que l'on retrouvera, on obtiendra donc bien rigoureusement le même résultat géométrique que si l'on avait pu générer un seul TIN sur l'ensemble des données (TIN couvrant l'intégralité de la dalle).
La seule contrainte pour l'utilisateur avec cette approche est de définir l'amplitude de la zone de recouvrement :
•Si cette zone est trop petite par rapport à la distance moyenne entre les points, on risque fort de ne pas intégrer les points permettant de générer les triangles en chevauchement.
•Si la zone de recouvrement est trop grande, on aura intégré beaucoup trop de points, plus que nécessaire pour créer tous les triangles en chevauchement.
•Enfin, si la zone de recouvrement est vraiment trop importante, on risque d'obtenir dans la zone de recouvrement elle-même plus de points que la mémoire disponible n'est capable de traiter, même après une infinité de découpages aboutissant à une taille de dalle quasiment nulle.
En théorie, la valeur de l'amplitude de la zone de recouvrement devrait donc être égale à la longueur maximale d'une arête de triangle, soit la distance maximale entre deux points utilisés dans la création d'un même triangle.
Dans les paramètres par défaut :
•Une distance de -1 signifie que la distance de recouvrement est calculée automatiquement par le logiciel.
•Une distance de 0 signifie que la distance de recouvrement est infinie.
En pratique, il est souvent impossible de repérer dans de gros volumes de données cette distance maximale. On se contente donc de repérer une zone de données la moins dense possible, de mesurer la distance pouvant être cette distance maximale entre deux points, et d'appliquer à cette distance un coefficient de sécurité de par exemple 1.2, ou 1.5 ou 2 selon la mémoire disponible. Si la mémoire disponible est très limitée, on devra prendre soin d'utiliser un coefficient minimal pour éviter que la zone de recouvrement ne contienne à elle seule un nombre de points trop important. Si à l'inverse, la mémoire disponible est importante, et donc que le nombre de points dans la zone de recouvrement est peu significatif par rapport à cette mémoire disponible, on pourra se permettre d'appliquer un coefficient plus important.
Voici un exemple pour illustrer la démarche.
Sur ce jeu de données (Exemple de jeu de données ci-après), où l'on a mesuré 1311 mètres entre deux courbes de niveau significatives de l'écart maximal, on peut espérer qu'un recouvrement de 1500 mètres sera suffisant, et si on a une mémoire disponible conséquente, on pourra se sécuriser en fixant un recouvrement à 2000 mètres.
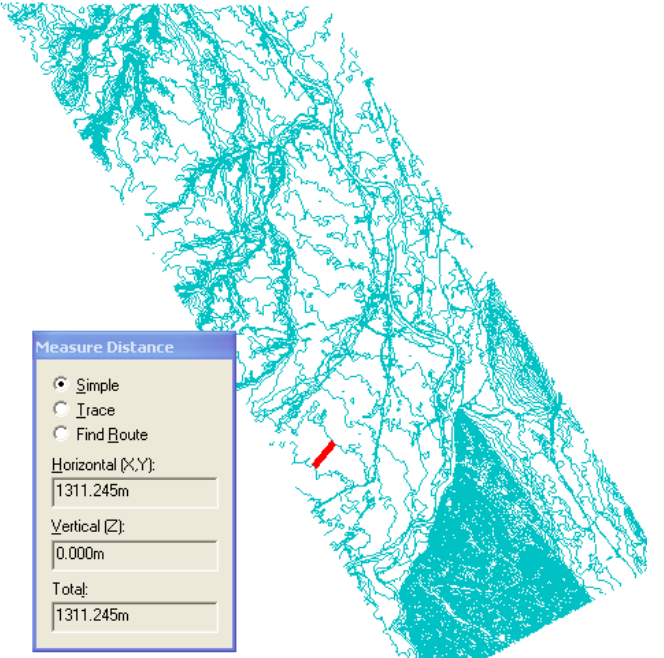
Exemple de jeu de données
Dans cet exemple, pour lequel on a vu précédemment qu'un recouvrement de 1500m devrait suffire, un recouvrement de 2000m a été utilisé. On visualise le découpage en dalles réalisé (en bleu), ainsi que la zone de recouvrement de chacune des dalles (en rouge).
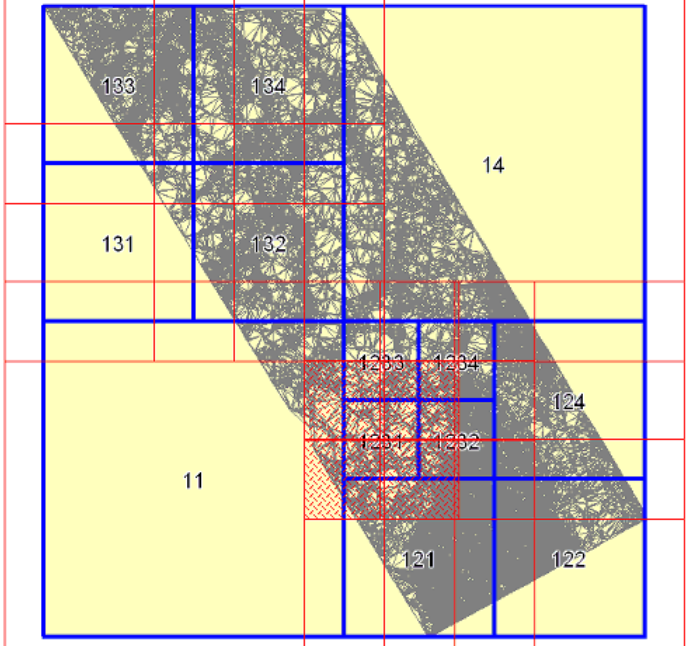
Découpage en dalles et zones de recouvrement des dalles
On visualise ici avec des couleurs différentes les TIN créés pour chacune des dalles. Les triangles qui chevauchent les limites des dalles se retrouvent dans au moins deux TIN.
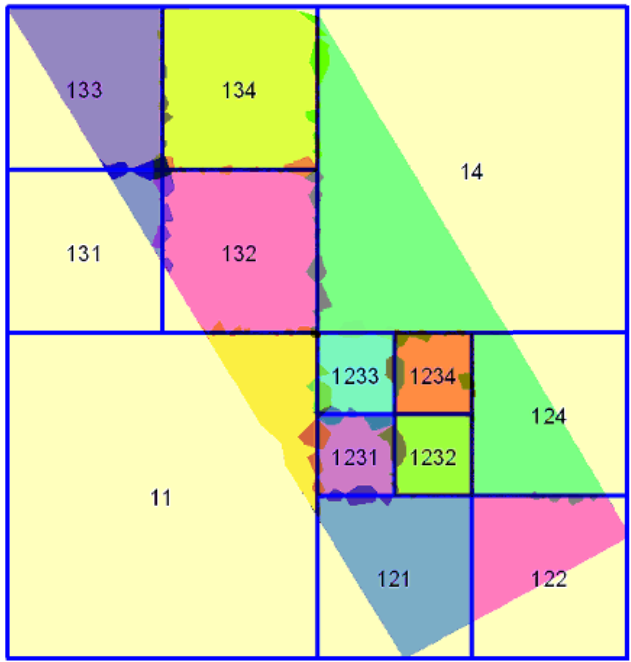
TIN créés
Mais géométriquement, on obtient le même résultat que si la triangulation avait été faite en un seul TIN.

Modèle unique
Au final, si cette définition de l'amplitude du recouvrement est une opération un peu contraignante nécessitant d'examiner les données avant de les traiter, les algorithmes en tirent profit également pour supprimer tous les triangles en bordure de chaque TIN dont la longueur du plus grand coté excède la valeur de recouvrement. Ceci permet ainsi d'éliminer tous les triangles "parasites" situés dans les zones concaves des données sources. Il est possible de désactiver cette option de filtrage des triangles en fonction de leur longueur.