|
<< Cliquer pour afficher la table des matières >> Helmert - Recaler une image |
  
|
|
<< Cliquer pour afficher la table des matières >> Helmert - Recaler une image |
  
|
Cette fonction est accessible à la sélection d'un objet depuis le groupe Modification | Helmert dans le ruban Géométrie.
![]()
Utilité
La fonction Helmert est très utile pour géoréférencer une image ou un objet vectoriel. Elle permet notamment de créer un projet à partir d'une image d'un plan.
Principe
La fonction Helmert permet d'appliquer trois transformations à un objet vectoriel ou à une image :
•Une translation en X et en Y
•Une rotation
•Une mise à l'échelle
Les paramètres de cette transformation sont spécifiés par l'utilisateur en définissant deux vecteurs dans le cas d'un objet vectoriel et quatre vecteurs dans le cas d'une image.
Ces vecteurs permettent d'associer un point de l'objet à un point de référence.
Exemple avec un objet vectoriel
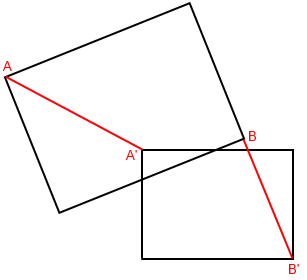
Helmert - Transformation d'un objet vectoriel
Dans l'exemple ci-dessus, le rectangle a été transformé selon les vecteurs définis par AA' et BB'.
Exemple avec une image
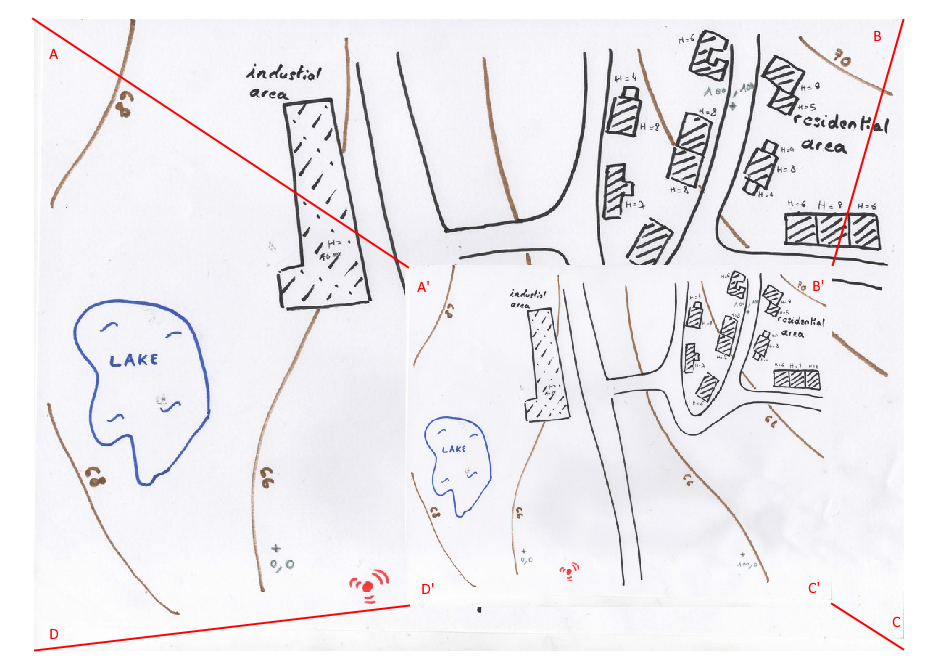
Helmert - Transformation d'une image
Dans l'exemple ci-dessus, l'image a été transformée selon les vecteurs définis par AA', BB', CC', DD'.
Définition des vecteurs
Une fois avoir sélectionné l'objet à transformer et activé la fonction Helmert, il faut spécifier les vecteurs. Deux vecteurs dans le cas d'un objet vectoriel, quatre vecteurs dans le cas d'une image.
Pour cela :
•Définition du premier vecteur :
oCliquer un premier point sur l'objet à transformer
oCliquer le point correspondant sur la référence
•Définition du second vecteur :
oCliquer un premier point sur l'objet à transformer
oCliquer le point correspondant sur la référence
La transformation Helmert s'applique.
Dans le cas où l'on souhaite transformer une image, deux vecteurs supplémentaires sont nécessaires.
•Définition du troisième vecteur :
oCliquer un premier point sur l'image à transformer
oCliquer le point correspondant sur la référence
•Définition du quatrième vecteur :
oCliquer un premier point sur l'image à transformer
oCliquer le point correspondant sur la référence
La transformation Helmert s'applique.